SOMMAIRE

Après les vacances, le 6 ou le 9 Mai (selon votre groupe de TD), vous aurez un TP noté portant sur Open GL. Pour ce TP noté, les règles sont les suivantes :

• Vous pourrez travailler seul ou à 2 étudiants (binôme mais pas plus)
• Tous les supports de cours ainsi que les corrections des TP OpenGL seront autorisés et mis en ligne d'ici là.
• Votre travail devra être déposé en fin de séance sur moodle.
• Vous devez venir avec votre carte d'étudiant, ou à défaut une pièce d'identité.
• Vous devez respecter votre groupe de TD afin que chacun puisse avoir une machine pour travailler

Ne pas hésiter à me poser les questions que vous auriez concernant cette évaluation.

Partie 1 : approximation polyédrique

Partie 2 : opérations sur les sommets : animation par transformations de modèle

Partie 3 : callbacks

Partie 4 : opérations sur les pixels : application de textures

Exercices supplémentaires

Note de CC 2018/2019 : projet à réaliser

TP noté 2021/2022

Corrections

Partie 1 : approximation polyédrique

Exercice 1 : déterminer les sommets d'un polyèdre.

• Un carré dont les arêtes sont de taille 1.
• Un cube dont les arêtes sont de taille 1.
• Une pyramide dont la base est constituée d'un carré ayant des arêtes de taille 1. Vous indiquerez sur vos figures le repère cartésien.
  

Exercice 2 : écrire un programme qui dessine un polygone

Figure 1. Ajouter un triangle rouge

Exercice 3 : écrire un programme qui dessine un polyèdre

On vous demande maintenant d'écrire les programmes qui affichent différents polyèdres. Pour ce faire, récupérer tous les fichiers de cet exercice à partir de ce répertoire. Vous les stockerez tous dans un répertoire que vous nommerez EXO3. Ces fichiers s'utilisent comme ceux de l'exercice précédent.

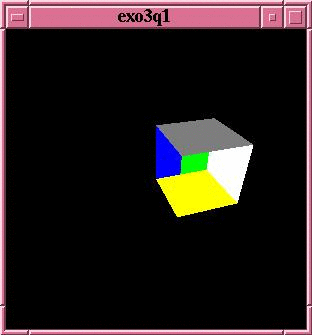
Figure 2. Un cube

1. Modifier le fichier display.c en ajoutant dans la fonction display() la restitution d'un cube dont les faces de taille 1 seront jaune, blanche, bleue, rouge, grise et verte (cf. Figure 2).
2. Pourquoi voit-on, par transparence, certaines faces du cube ? Dites quel traitement graphique corrige cette erreur et comment on peut modifier le programme à cet effet.

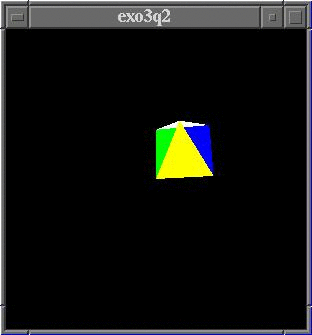
Figure 3. Une pyramide

3. Refaire l'exercice mais en substituant le cube par une pyramide de taille 1 et dont les faces seront jaune, blanche, bleue, rouge et verte (cf. Figure 3).

Figure 4. Un cylindre

4. Faites de même en substituant la pyramide par un cylindre de taille 1 dont les faces sont jaune, bleue et blanc (cf. Figure 4). On vous demande de réaliser cet objet en respectant les étapes suivantes:

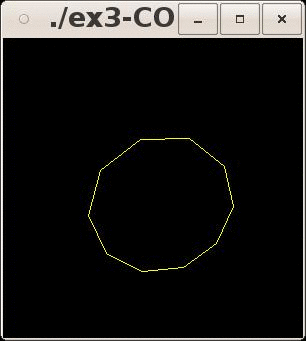
1.      D'abord, écrire le code qui trace un décagone sur le plan z=0 (cf. Figure ci-dessous). Votre décagone sera tracé en mode filaire. Le mode filaire est activé en ajoutant dans votre programme l'instruction glPolygonMode(GL_FRONT_AND_BACK, GL_LINE).

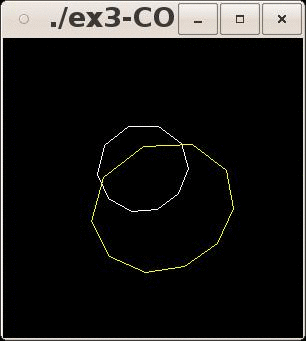
2. Puis, modifier votre programme afin qu'il trace un second décagone sur le plan z=1 (cf. Figure ci-dessous).

3. Puis, modifier votre programme afin qu'il trace UN quadrilatère reliant les deux décagones.

4. Puis, modifier votre programme afin qu'il trace TOUS les quadrilatères reliant les deux décagones.

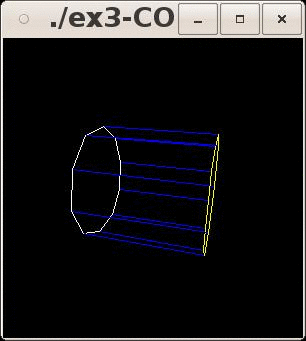
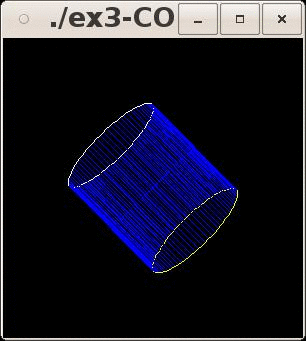
5. Enfin, modifier votre programme afin de ne plus afficher des décagones mais des approximations de cercle constituées de 60 points. Pour afficher votre cylindre avec des polygones coloriés, n'oubliez pas de supprimer la commande glPolygonMode(GL_FRONT_AND_BACK, GL_LINE).

Exercice 12 : approximations de sphère

#define X .525731112119133606
#define Z .850650808352039932

GLfloat sommets[12][3] =
{
  {-X, 0, Z},
  {X, 0, Z},
  {-X, 0, -Z},
  {X, 0, -Z},
  {0, Z, X},
  {0, Z, -X},
  {0, -Z, X},
  {0, -Z, -X},
  {Z, X, 0},
  {-Z, X, 0},
  {Z, -X, 0},
  {-Z, -X, 0}
};

int polygon_index[20][3] =
{
  {0, 4, 1},
  {0, 9, 4},
  {9, 5, 4},
  {4, 5, 8},
  {4, 8, 1},
  {8, 10, 1},
  {8, 3, 10},
  {5, 3, 8},
  {5, 2, 3},
  {2, 7, 3},
  {7, 10, 3},
  {7, 6, 10},
  {7, 11, 6},
  {11, 0, 6},
  {0, 1, 6},
  {6, 1, 10},
  {9, 0, 11},
  {9, 11, 2},
  {9, 2, 5},
  {7, 2, 11},
};

1. Le code source pour le programme de cet exercice peut être récupéré à partir de ce répertoire. Vous sauvegarderez ces fichiers dans le répertoire EXO12.
2. Ecrire une fonction void draw_triangle(float* v1, float *v2, float *v3) qui dessine un triangle dont les sommets ont les coordonnées (x,y,z) suivantes : (v1[0], v1[1], v1[2]), (v2[0], v2[1], v2[2]) et (v3[0], v3[1], v3[2]).
3. Compléter le programme afin de restituer un icosaèdre (cf. exécutable exo12q1 ). La fonction d'affichage de ce programme consiste a créer 20 triangles en utilisant la fonction draw_triangle. Le programme implémente une animation qui consiste en une rotation de la sphère par transformation de modèle. Afin de pouvoir apprécier le volume de la sphère, les triangles doivent être remplis par un dégradé de couleur.
4. Une méthode possible pour approximer une sphère à partir d'un icosaèdre consiste à diviser chaque triangle en 4 triangles. Chaque nouveau triangle peut ensuite être à nouveau divisé jusqu'à l'obtention de la sphère recherchée. L'exécutable exo12q2 montre un icosaèdre où ce processus récursif de division à été appliqué 3 fois (il y a donc 20*4*4*4=1280 triangles).
   
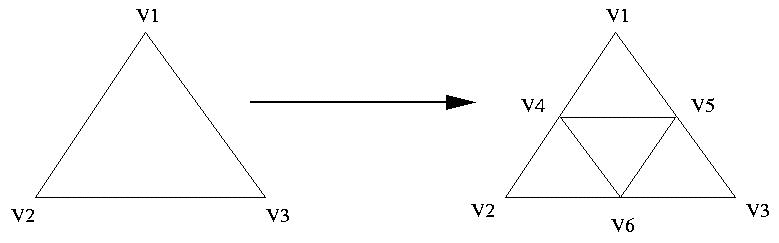
   Division de triangle
   
   
   
   L'algorithme de division fonctionne comme suit (cf. figure ci-dessus) :
   • On calcule les coordonnées (x,y,z) des trois nouveaux sommets V4, V5, V6 à l'aide des coordonnées (x,y,z) des sommets initiaux V1, V2, V3. Par exemple, soit (xv1,yv1,zv1) et (xv2,yv2,zv2) les coordonnées de V1 et V2, les coordonnées de V4 sont calculées par : xv4=(xv1+xv2)/2, yv4=(yv1+yv2)/2, et zv4=(zv1+zv2)/2.
   • Une fois que sont calculées les coordonnées (x,y,z) de chaque nouveau sommet (c'est à dire V4, V5, V6), leurs coordonnées doivent être normalisées en invoquant la fonction calcul_normal.

     void calcul_normal(float v[3])
     {
             float d=sqrt(v[0]*v[0]+v[1]*v[1]+v[2]*v[2]);
             v[0]=v[0]/d;
             v[1]=v[1]/d;
             v[2]=v[2]/d;
     }
     

   • Enfin on dessine avec les primitives géometriques d'OpenGL les nouveaux triangles ainsi définis.
   
   
   
   
5. Ecrire une version récursive de la fonction void draw_triangle(float* v1, float *v2, float *v3, int iteration) qui affiche un triangle et ses sous-triangles en éventuellement exécutant cet algorithme de division récursive. iteration est le niveau de récursion (et donc le nombre de division) souhaité.

Partie 2 : operations sur les sommets : animation par transformations de modèle

Dans cette partie, on souhaite aborder la problématique de l'animation.

Dans les exercices précédents, nous avons focalisé notre attention sur la description et la restitution d'une image fixe. En effet, certains des programmes qui nous avons étudiés fonctionnaient de sorte que toutes les 40 millisecondes, la fonction display était exécutée afin de re-dessiner une scène identique. Pour qu'une animation soit réalisée, il suffit que deux exécutions successives de la fonction display ne dessinent pas une scène identique.
Dans les exercices suivants, les programmes que nous écrirons comporteront une fonction display décrivant une scène qui évoluera dans le temps.

Transformations de modèle

Pour réaliser une animation, on utilise généralement des outils qui transforment le système de coordonnées : ce sont les primitives de transformations de modèle glTranslatef, glRotatef et glScalef. Ces primitives effectuent différentes opérations algébriques sur les sommets du modèle (les opérations sur les sommets sont basés sur l’algèbre matricielle, cf. cours magistral). Ces primitives fonctionnent comme suit :

1. glTranslatef(tx,ty,tz) : déplace le système de coordonnées selon le vecteur de translation (tx, ty, tz). Par la suite, tout point dessiné grâce à la primitive glVertex3f sera dessiné conformément à la nouvelle position du système coordonnées.
2. glRotatef(angle, rx,ry,rz) : applique au système de coordonnées une rotation sur un angle en degrés dont la valeur est angle sur l'axe définit par le vecteur (rx, ry, rz). Par la suite, tout point dessiné grâce à la primitive glVertex3f sera dessiné conformément à la nouvelle orientation du système de coordonnées.
3. gScalef(sx,sy,sz) : effectue une mise à l'échelle du système de coordonnées sur un ou plusieurs de ses axes (x et/ou y et/ou z). sx, sy et sz sont les facteurs de mise à l'échelle pour chaque axe. Ainsi, si sx>1, alors l'abscisse est élargi. Si sx<1, elle est rétrécie. Les trois axes peuvent être rétrécis ou élargis de façon indépendante. Par la suite, tout point dessiné grâce à la primitive glVertex3f sera dessiné conformément à la nouvelle taille du système coordonnées.

Dans les exercices suivants, nous allons expérimenter ces primitives.

Exercice 4 : exemple élémentaire d'animation

Pour votre première animation, on vous demande d'étudier le programme présenté en cours. Vous pouvez récupérer le programme dans ce répertoire. Vous stockerez ce programme dans un répertoire nommé EXO4. Dans ce programme, un carré rouge est dessiné. On applique à ce carré une rotation selon l'axe des x.

1. Identifier dans le programme l'instruction qui modifie le système de coordonnées afin d’implanter cette rotation.
2. Modifier ce programme afin que la rotation soit deux fois plus rapide que la vitesse actuelle.
3. Que se passe t il lorsque la variable xRotation dépasse la valeur 360 ?

Exercice 5 : mise à l'échelle

Dans cet exercice, on teste le fonctionnement de glScalef. Soit l'exécutable exo5. On vous demande de :

1. Tester le programme exo5. L'animation consiste à modifier la taille du cube de 10 pourcents à chaque exécution de la fonction display. Initialement, le cube est de taille 1. Lorsque le cube dépasse la taille 4, alors sa taille doit être positionnée à sa taille d'origine (arête de taille 1).
2. Compléter la fonction display afin d'effectuer cette animation. Le code source du programme à compléter peut être récupéré à partir de ce répertoire.  Vous sauvegarderez ces fichiers dans le répertoire EXO5.

Exercice 6 : translation + rotation

Dans cet exercice, on réalise une animation constituée d’une translation et d’une rotation (opérations réalisées par les fonctions glTranslatef() et glRotatef()).

1. Soit l'exécutable exo6q1. Proposez un programme qui effectue cette animation. Le cube est de taille 1. Pour faire cette animation, il est nécessaire de faire une rotation sur l'axe des x. Vous devez partir du programme stocké dans ce répertoire. Nota bene : les dégradés de couleur d'un polygone sont obtenus en spécifiant des couleurs différentes pour les différents sommets du polygone.
2. Récupérez cette nouvelle version de l'exécutable exo6q2 et modifiez votre programme précédent afin d'effectuer cette nouvelle animation. Cette animation combine la rotation de la question précédente avec une translation sur l’axe des z.  L’objet doit se déplacer entre les plans z=0 et z=10.

Exercice 7 : construction hiérarchique d’une scène par transformation de modèle

On souhaite construire une scène grâce à des transformations de modèle et la pile de matrice de modélisation (glTranslatef(), glPopMatrix() et glPushMatrix()).

La scène à construire est un damier (matrices 10x10 de carrés blancs et noirs) sur un fond d'écran bleu. Le positionnement des objets est réalisé par des déplacements du système de coordonnées. On vous donne la fonction carre(). Cette fonction dessine un carré de taille 1. Les paramètres de cette fonction définissent la couleur de carré. L’exécutable à obtenir est celui-ci.
Le code source du programme à compléter peut être récupéré à partir de ce répertoire.  Vous sauvegarderez ces fichiers dans le répertoire EXO7.

On vous demande :

1.      De tester l’exécutable.

2.      Puis, de compléter la fonction  display() afin d’afficher UNE ligne de 10 carrés (cf. figure ci-dessous). Vous ne devez par modifier la fonction carre(): il faudra donc utiliser glTranslatef() pour déplacer le système de coordonnées.

3.      Enfin, de modifier votre programme afin d’afficher 10 lignes de 10 carrés  Pour passer d’une ligne à une autre, il sera nécessaire d’utiliser glTranslatef() ainsi que glPushMatrix() et glPopMatrix().

Exercice 8 :

Soit l'exécutable exo8. Proposez un programme qui réalise cette animation. Le déplacement du cercle doit être effectué par une transformation de modèle (glTranslate).

Partie 3 : callbacks

Exercice 11

1. Restitue un cube.
2. Modifie l'aspect du cube de la façon suivante :
   • Lorsque l'utilisateur frappe la touche l (respectivement L), sa dimension sur l'axe x est multipliée par deux (respectivement divisée par deux).
   • Lorsque l'utilisateur frappe la touche h (respectivement H), sa dimension sur l'axe y est multipliée par deux (respectivement, divisée par deux).
   • Lorsque l'utilisateur frappe la touche p (respectivement P), sa dimension sur l'axe z est multipliée par deux (respectivement, divisée par deux).
   • Lorsque l'utilisateur frappe la touche v (respectivement V), ses dimensions sur les axes x,y et z) sont multipléess par deux (respectivement, divisées par deux).
3. Testez le programme en appuyant sur les touches 'z', 'Z', 'y', 'Y', 'x' et 'X'. A votre avis, que fait la fonction gluLookAt.

Exercice 13

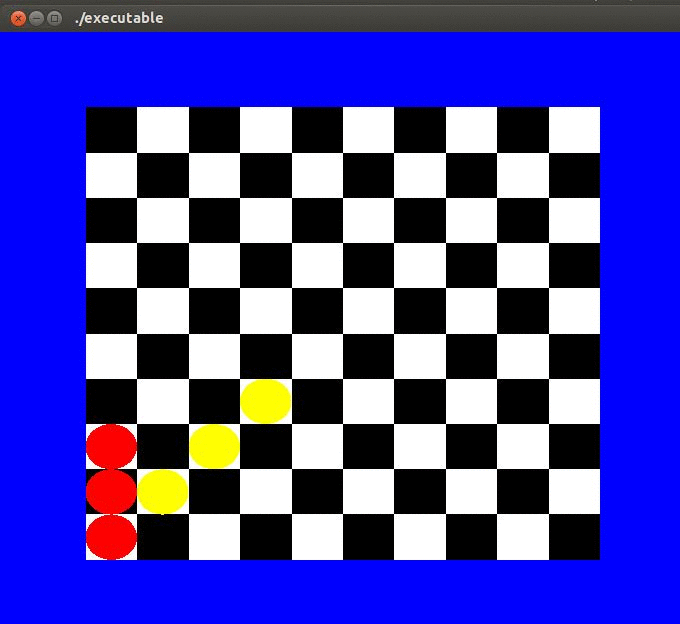
Damier et pions rouges et jaunes

• Au départ le damier affiché est vide.
• L'utilisateur choisit le numéro de ligne (de 0 à 9) en frappant la touche correspondante.
• Puis, il choisir le numéro de colonne.
• Enfin, il frappe soit la touche 'r', soit la touche 'j' pour afficher le nouveau pion rouge ou jaune. Pour ce faire, il suffit d'ajouter le nouveau pion dans les tableau position_rouge ou position_jaune.

Parties 4 : opérations sur les pixels : application de textures

Exercice 9 : testez les outils offerts par OpenGl pour appliquer des textures

1. Compilez, testez puis étudiez le programme.
   
   

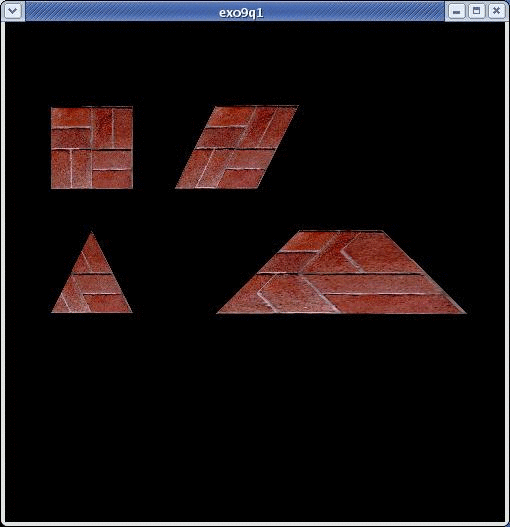
2. Modifiez le programme en ajoutant les polygones de la figure ci-dessus auxquels vous appliquerez la texture brick10.ppm.
   

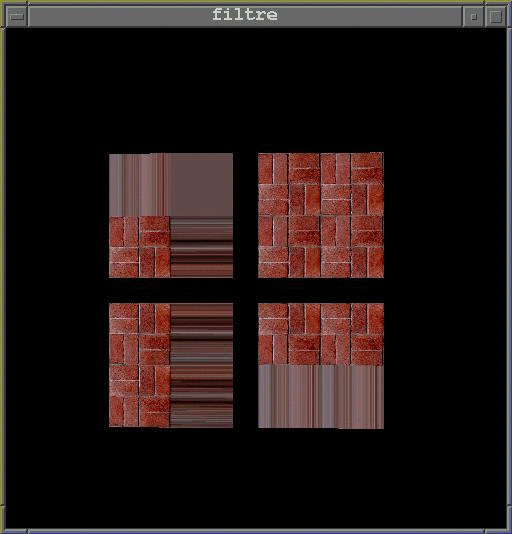
3. Modifiez le programme de sorte que quatre carrés soient restitués avec la même texture mais en paramètrant l'objet de texture de sorte que l'extrapolation de texels soit effectuée comme dans la figure ci-dessus.
   

4. Modifiez le programme de sorte que trois carrés soient restitués avec la même texture mais en paramétrant la texture de sorte que soit successivement utilisé les trois principales méthodes de combinaison de couleurs (respectivement GL_REPLACE, GL_ADD et GL_MODULATE). Le polygone à texturer est jaune.

Exercice 10 : textures par blocs de texels

1. Dans un premier temps, on vous demande de compléter le fichier display afin d'obtenir un ensemble de polygones présentés en mode fil de fer (c'est à dire non coloriés). Soit l'exécutable exo10q1 . Ecrire un programme qui implante la scène présentée par cet exécutable :
   • Il s'agit d'un tunnel constitué d'un ensemble de rectangles.
   • L'animation est réalisée par un déplacement de la caméra le long de l'axe z de 0 à -40. L'animation est déjà implantée, il ne vous reste plus qu'à définir les polygones.
   • Différents rectangles constituent les murs gauches et droits ainsi que le plafond et le plancher.
   • Un ensemble de rectangles modélisent des fenêtres sur les murs ainsi que des tapis sur le plancher.
   • Enfin, des polygones positionnés en haut des murs représentent des frises.
2. Dans un deuxième temps, on se propose de plaquer des textures sur le modèle fil de fer élaboré dans la question précédente. Pour ce faire, vous disposez des textures suivantes.
3. Modifiez votre programme de sorte que le résultat restitué par votre programme soit similaire à celui de l'exécutable exo10q2 .

Exercices supplémentaires

Note de CC 2017/2018 : projet à réaliser

Figure. Jeu du puissance 4 en 3D

• Il y a 32 boules claires et 32 boules foncées.
• Le plateau contient 16 tiges. Chaque tige peut contenir 4 boules.
• Pour gagner, un joueur doit aligner 4 boules. Les boules peuvent être alignées horizontalement, verticalement ou en diagonale et sur n'importe quel étage des tiges.
• La partie est nulle si toutes les boules sont posées et si aucun joueur n'a réussi à aligner 4 boules.

• Le projet devra être remis le 2 Mai par mail à Frank Singhoff. Une démonstration sera également organisée les 3 et 4 Mai.
• Vous serez évalués sur les critères suivants : les fonctionnalités, la conception détaillée, l'état d'avancement, les techniques et effets graphiques utilisés, la qualité du code (propreté, fiabilité), la documentation.
• Vous devez au minimum réaliser la scène (présentation des différents objets). La mise en oeuvre complète du jeu (détection de fin de partie) constituera un plus pour la notation.
• La qualité de la documentation sera prépondérante pour la notation : votre documentation devra comporter un petit manuel d'utilisation et une description de la conduite des tests.
• Vous devez obligatoirement utiliser le matériel/logiciel utilisé pendant les cours : vous ne devrez pas utiliser de code autre que celui offert par les bibliothèques gl, glu et glut (pas de code téléchargé depuis le web !) sur Linux uniquement.
• Les démonstrations seront effectuées sur les machines de salles de TP. Les projets utilisant d'autres plate-formes de développement ne seront pas évalués. Vous pouvez travailler seul, à deux ou à trois étudiants.

Note de CC 2016/2017 : projet à réaliser

1. Utilisation des primitives géométriques,
2. Transformation de modèle.

Figure. Exemples de Pacman

• Lors du cours du 25 avril, il vous sera demandé de montrer une première version de votre projet où l'on vous demande d'implanter au minimum la description de scène.
• Le projet devra être remis le 5 Mai par mail à Frank Singhoff. Une démonstration sera également organisée le 5 Mai après midi.
• Vous serez évalués sur les critères suivants : les fonctionnalités, la conception détaillée, l'état d'avancement, les techniques et effets graphiques utilisés, la qualité du code (propreté, fiabilité), la documentation.
• La qualité de la documentation sera prépondérante pour la notation : votre documentation devra comporter un petit manuel d'utilisation et une description de la conduite des tests. Vous devez obligatoirement utiliser le matériel/logiciel utilisé pendant les cours : vous ne devrez pas utiliser de code autre que celui offert par les bibliothèques gl, glu et glut (pas de code téléchargé depuis le web !) sur Linux uniquement. Les démonstrations seront effectuées sur les machines de salles de TP. Les projets utilisant d'autres plate-formes de développement ne seront pas évalués.
• Vous pouvez travailler seul ou en groupe de 2 à 3 étudiants (mais pas a plus de 3 étudiants).

Note de CC 2018/2019 : projet à réaliser

1. Utilisation des primitives géométriques,
2. Opérations sur les sommets (transformations).

Figure. Différents exemples de Rubik's cube