TP openGl

UE Multimédia et animation

Frank Singhoff

SOMMAIRE



Déroulement des TPs:
La série de TP est organisée en trois parties principales. Dans un premier temps sont présentées les fonctionnalités permettant la restitution d'objets 2D et 3D élémentaires. La deuxième partie traite des transformations. Enfin, nous terminons par l'étude des textures et de l'éclairage.





I. Primitives géométriques et techniques d'animation élémentaires



Avant d'exécuter les programmes ci-dessous, vous devez definir la variable shell suivante :

setenv MESA_PATH /home/commun_depinfo/enseignants/singhoff/Mesa
setenv LD_LIBRARY_PATH $MESA_PATH/lib:$LD_LIBRARY_PATH

On suppose ici que vous utilisez tcsh ou csh.

D'autre part, vous disposez des documentations suivantes qui contiennent les services nécessaires à l'élaboration des programmes ci-dessous: Ainsi que d'un ensemble d'exemples:


Ce TP est basé d'après un ouvrage de référence sur OpenGL dont une version antérieure est distribuée au format électronique.




Enfin, pour compiler un programme C tel que mon_programme.c, vous utiliserez la commande :

gcc -I$MESA_PATH/include mon_programme.c -o mon_programme -L$MESA_PATH/lib -lGL -lGLU -lglut -L/usr/X11R6/lib -lX11





Exercice 1 : premier exemple de programme OpenGl

  1. Compilez et testez le programme exo1.c. Ce programme utilise le simple buffering (primitive glFlush et intialisation de la GLUT avec GLUT_SINGLE). L'utilisation du double buffering nécessite l'utilisation de la primitive glutSwapBuffers et l'initialisation de la GLUT avec GLUT_DOUBLE).
  2. Avec quelle primitive géométrique le carré est il dessiné ? quelle autre primitive aurions nous pu utiliser ?




Exercice 2 : technique élémentaire d'animation


Figure 1. Ajouter un triangle rouge


  1. Modifiez le programme de l'exercice 1 de sorte que celui-ci dessine un triangle rouge comme indiqué dans la figure 1.
  2. On souhaite mettre en place une animation simple qui consiste à changer la couleur du carré toutes les 1 milliseconde. Grâce à glutTimerFunc, mettre en place cette animation. Les couleurs affichées doivent se succéder de sorte que toutes les 1 milliseconde une composante R, G ou B est incrémentée de 0.25 points.
  3. Quelle est la raison pour laquelle l'animation pourrait ne pas être nette ? Modifiez le programme de façon à supprimer cet effet indésirable.




Exercice 3 : modèles d'objets 3D élémentaires


Figure 2. Un cube

Soit le programme exo3.c
  1. Compilez et testez ce programme. Ce programme effectue une animation par timer.
  2. Modifiez le programme en ajoutant dans la fonction display la restitution d'un cube dont les faces de taille 1 seront jaune, blanche, bleue, rouge, grise et verte (cf. Figure 2). Vous n'utiliserez pas les fonctions de la GLUT pour construire ce cube.
  3. Pourquoi voit-on, par transparence, certaines faces du cube ? Ajouter le code nécessaire au traitement graphique qui corrige cette erreur.


    Figure 3. Une pyramide

  4. Faites de même en substituant le cube par une pyramide de taille 1 dont les faces seront jaune, blanche, bleue, rouge et verte (cf. Figure 3).


    Figure 4. Un cylindre

  5. Faites de même en substituant le cube par un cylindre de taille 1 jaune et blanc (cf. Figure 4). Pour faire cet objet, tracez 2 cercles puis plusieurs quadrilatères reliant les deux cercles.






II. Les transformations de scène





  • Avant de commencer le TP, récupérez et testez les programmes de Nate Robins :
    1. projection : ce programme vous permet de tester le fonctionnement des primitives liées aux tranformations de projection et de visualisation d'OpenGl.
    2. transformation : ce programme vous permet de tester le fonctionnement des primitives liées aux tranformations de modèle d'OpenGl.


    Pour tester ces programmes, cliquez sur les paramètres et déplacez la souris pour faire évoluer leur valeur.







    Exercice 4 : transformation de modèle : mise à l'échelle



    Dans cet exercice, on teste le fonctionnement de glScale. Soit l'exécutable exo4 et le source exo4.c. Ecrire le code de ce programme qui :
    1. Restitue un cube.
    2. Modifie l'aspect du cube de la façon suivante :
      • Lorsque l'utilisateur frappe la touche l (respectivement L), sa dimension sur l'axe x est multipliée par deux (respectivement divisée par deux).
      • Lorsque l'utilisateur frappe la touche h (respectivement H), sa dimension sur l'axe y est multipliée par deux (respectivement, divisée par deux).
      • Lorsque l'utilisateur frappe la touche p (respectivement P), sa dimension sur l'axe z est multipliée par deux (respectivement, divisée par deux).
      • Lorsque l'utilisateur frappe la touche v (respectivement V), ses dimensions sur les axes x,y et z) sont multipléess par deux (respectivement, divisées par deux).
    3. Testez le programme en appuyant sur les touches 'z', 'Z', 'y', 'Y', 'x' et 'X'. A votre avis, que fait la fonction gluLookAt.




    Exercice 5 : transformation de modèle : translation

    Soit l'exécutable exo5. Proposez un programme qui réalise cette animation. Le déplacement du cercle doit être effectué par une transformation de modèle (glTranslate) .



    Exercice 6 : transformation de modèle vs transformation de visualisation

    Dans cet exercice, on montre qu'il est possible de combiner une transformation de modèle (glRotate et glTranslate) et une transformation de visualisation (gluLookAt). Soit l'exécutable exo6q1.
    1. Proposez un programme qui effectue l'animation de rotation par une transformation de modèle. Nota bene : les dégradés de couleur d'un polygone sont obtenus en spécifiant des couleurs diffférentes pour chaque sommet du polygone.
    2. Récupérez cette nouvelle version de l'exécutable exo6q2. Il est possible de réaliser l'animation qui consiste à déplacer l'objet par une transformation de visualisation et une transformation de modèle (déplacement de la caméra et rotation de l'objet). Proposez un programme qui restitue cette animation. Nota bene : la transformation de visualisation pourrait aussi être remplacée par une translation (cad une transformation de modèle).




    Exercice 7 : construction hiérarchique de scène par transformation de modèle


    Figure 5. Le damier

    1. On souhaite construire une scène grâce à des transformations de modèle (glRotate, glTranslate, glScale, glPopMatrix et glPushMatrix).

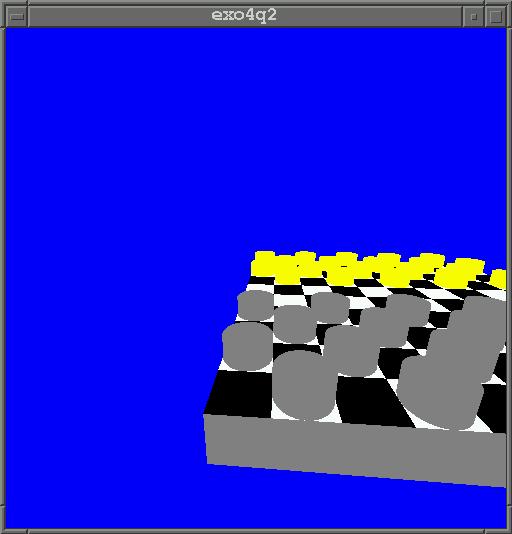
      La scène à construire est un damier (matrices de 10x10 de cubes blancs et noirs) sur un fond d'écran bleu. Le programme a obtenir est celui-ci. Le damier comporte 20 pions jaunes et gris foncé (une tranche de cylindre). Les pions sont placés sur les cases claires en 4 rangées.

      Le positionnement des objets est réalisé par des déplacements de l'origine ; les fonctions qui dessinent effectivement les objets (cubes et cylindres) le font systèmatiquement centré sur l'origine. Pour ce faire, vous devez :
      • Ecrire deux fonctions C :
        1. La première fonction trace un cube centré sur l'origine. La fonction doit être paramétrée par la couleur du cube à restituer.
        2. La deuxième fonction trace un pion centré sur l'origine. La fonction doit être paramétrée par la couleur du pion à restituer.
      • Tracer les cases du damier à l'aide de la fonction qui dessine le cube centré. Vous utiliserez glTranslate pour positionner l'origine à l'emplacement des cases à dessiner. glPushMatrix et glPopMatrix doivent être utilisés pour replacer l'origine à sa place initiale lorsque l'on a terminé de dessiner une ligne par exemple.
      • Tracer les pions clairs et foncés avec la même méthode.
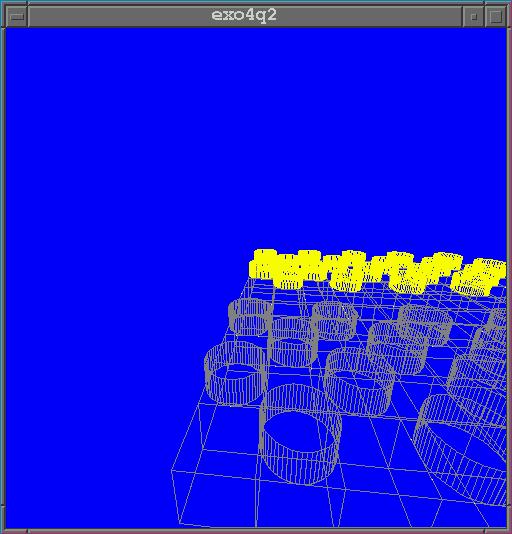
      • Modifier votre programme afin de tester la fonction glPolygonMode. Cette fonction permet de ne pas remplir les polygones tracés.




      Exercice 8 : approximations de sphère

      Nous regardons maintenant comment approximer une sphère avec un polyèdre.

      Il est possible d'approximer un volume sphérique par un icosaèdre régulier (polyèdre étudié par Platon). Un icosaèdre est un polyèdre constitué de 20 triangles définis par 12 sommets. Le code C ci-dessous définit les triangles d'un icosaèdre : 
      
#define X .525731112119133606
#define Z .850650808352039932

GLfloat sommets[12][3] =
{
  {-X, 0, Z},
  {X, 0, Z},
  {-X, 0, -Z},
  {X, 0, -Z},
  {0, Z, X},
  {0, Z, -X},
  {0, -Z, X},
  {0, -Z, -X},
  {Z, X, 0},
  {-Z, X, 0},
  {Z, -X, 0},
  {-Z, -X, 0}
};

int sindex[20][3] =
{
  {0, 4, 1},
  {0, 9, 4},
  {9, 5, 4},
  {4, 5, 8},
  {4, 8, 1},
  {8, 10, 1},
  {8, 3, 10},
  {5, 3, 8},
  {5, 2, 3},
  {2, 7, 3},
  {7, 10, 3},
  {7, 6, 10},
  {7, 11, 6},
  {11, 0, 6},
  {0, 1, 6},
  {6, 1, 10},
  {9, 0, 11},
  {9, 11, 2},
  {9, 2, 5},
  {7, 2, 11},
};
      Ainsi, le premier triangle est défini par les trois sommets numéro 0, 4 et 1, c'est à dire par les sommets de coordonnées (-X,0,Z), (0,Z,X) et (X,0,Z).



      1. Ecrire une fonction void draw_triangle(float* v1, float *v2, float *v3) qui dessine un triangle dont les sommets ont les coordonnées (x,y,z) suivantes : (v1[0], v1[1], v1[2]), (v2[0], v2[1], v2[2]) et (v3[0], v3[1], v3[2]).
      2. Ecrire un programme qui restitue un icosaèdre (cf. exécutable exo8q1 ). La fonction d'affichage de ce programme consiste a créer 20 triangles en utilisant la fonction draw_triangle. Le programme implémente une animation qui consiste en une rotation de la sphère par transformation de modèle. Afin de pouvoir apprécier le volume de la sphère, les triangles doivent être remplis par un dégradé de couleur.
      3. Une méthode possible pour approximer une sphère à partir d'un icosaèdre consiste à diviser chaque triangle en 4 triangles. Chaque nouveau triangle peut ensuite être à nouveau divisé jusqu'à l'obtention de la sphère recherchée. L'exécutable exo8q2 montre un icosaèdre où ce processus récursif de division à été appliqué 3 fois (il y a donc 20*4*4*4=1280 triangles).


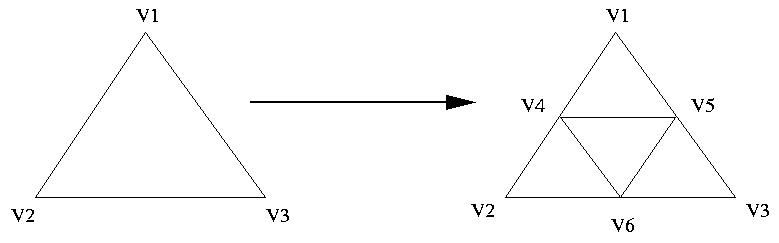
        Figure 6. Division de triangle




        L'algorithme de division fonctionne comme suit (cf. Figure 6) :
        • On calcule les coordonnées (x,y,z) des trois nouveaux sommets V4, V5, V6 à l'aide des coordonnées (x,y,z) des sommets initiaux V1, V2, V3. Par exemple, soit (xv1,yv1,zv1) et (xv2,yv2,zv2) les coordonnées de V1 et V2, les coordonnées de V4 sont calculées par : xv4=(xv1+xv2)/2, yv4=(yv1+yv2)/2, et zv4=(zv1+zv2)/2.
        • Une fois que sont calculées les coordonnées (x,y,z) de chaque nouveau sommet (c'est à dire V4, V5, V6), leurs coordonnées doivent être normalisées en invoquant la fonction calcul_normal. 
          void calcul_normal(float v[3])
{
        float d=sqrt(v[0]*v[0]+v[1]*v[1]+v[2]*v[2]);
        v[0]=v[0]/d;
        v[1]=v[1]/d;
        v[2]=v[2]/d;
}
        • Enfin on dessine avec les primitives géometriques d'OpenGL les nouveaux triangles ainsi définis.



      4. Ecrire une version récursive de la fonction void draw_triangle(float* v1, float *v2, float *v3, int iteration) qui affiche un triangle et ses sous-triangles en éventuellement exécutant cet algorithme de division récursive. iteration est le niveau de récursion (et donc le nombre de division) souhaité.






      III. Eclairage et application de texture

      Dans cette partie, on explore les outils liés aux textures et à l'éclairage. Afin de vous familiariser avec les primitives Open GL liées à ces services, vous pouvez aussi tester les programmes de Nate Robins (contenus dans le fichier tar donné dans la partie transformation). Ces programmes sont :
      • texture : montre les primitives de gestion des texture.
      • lightmaterial : montre les primitives permettant de définir les sources de lumières ainsi que la matière des objets.
      • lightposition : montre les primitives permettant de définir la position des sources de lumiere.




      Exercice 9 : testez les outils offerts par OpenGl pour appliquer des textures

      Dans cet exercice, on vous demande de tester les principales fonctionnalités d'application de textures. Soient les programmes exo9.c , ppm.c ainsi que le fichier de texture brick10.ppm .


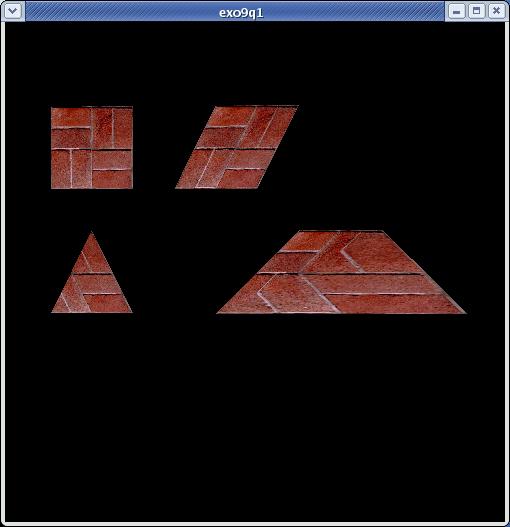
        Figure 8. Déterminer des coordonnées de textures

      1. Compilez, testez puis étudiez le programme exo9.c,
      2. Modifiez le programme exo9.c en ajoutant les polygones de la Figure 8 auxquels vous appliquerez la texture brick10.ppm.


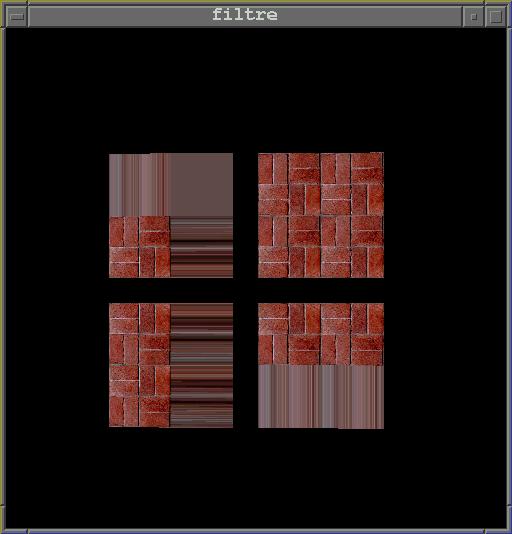
        Figure 9. Jouer avec l'extrapolation de texels

      3. Modifiez le programme exo9.c de sorte que quatre carrés soient restitués avec la même texture mais en paramètrant l'objet de texture de sorte que l'extrapolation de texels soit effectuée comme dans la Figure 9.


        Figure 10. Combiner les couleurs d'un polygone

      4. Modifiez le programme exo9.c de sorte que trois carrés soient restitués avec la même texture mais en paramétrant la texture de sorte que soit successivement utilisé les trois principales méthodes de combinaison de couleurs (respectivement GL_REPLACE, GL_ADD et GL_MODULATE). Le polygone à texturer est jaune.




      Exercice 10 : textures par blocs de texels

      Dans cet exercice, on vous demande d'appliquer différentes textures sur un modèle 3D.
      1. Dans un premier temps, on vous demande d'écrire un programme où les polygones sont restitués en mode filaire. Soit l'exécutable exo10q1 . Ecrire un programme qui implante l'animation de cet exécutable :
        • Il s'agit d'un tunnel constitué d'un ensemble de rectangles.
        • L'animation est réalisée par un déplacement de la caméra le long de l'axe z. En outre, vous pouvez visionner la scène en modifiant la position de la caméra grâce aux touches x, y et z.
        • Différents rectangles constituent les murs gauches et droits ainsi que le plafond et le plancher.
        • Un ensemble de rectangles modélisent des fenêtres sur les murs ainsi que des tapis sur le plancher.
        • Enfin, des polygones positionnés en haut des murs représentent des frises.
      2. Dans un deuxième temps, on se propose de plaquer des textures sur le modèle filaire élaboré dans la question précédente. Pour ce faire, vous disposez des textures suivantes. Celles-ci ont été téléchargées depuis ce site, puis, converties au format bitmap grâce à l'outil xv .
      3. Modifiez votre programme de sorte que le résultat restitué par votre programme soit similaire à celui de l'exécutable exo10q2 .




      Exercice 12 : exemple d'éclairage

      Dans cet exercice, on vous demande de tester un programme qui affiche une sphère approximée par un icosaèdre dans une scène où l'éclairage a été activé.
      1. Récupérez le programme exo12.c . Compilez, testez et étudiez ce programme.
      2. Afin de tester le comportement de chaque type de lumière, on vous demande de modifier ce programme de sorte que vous obteniez le comportement du programme exécutable exo12q1 suivant :
        • Si l'utilisateur presse la touche "s" (respectivement "S"), l'intensité de la lumière spéculaire de LIGHT0 est augmentée (respectivement diminuée). La variable concernée est light_specular.
        • Si l'utilisateur presse la touche "d" (respectivement "D"), l'intensité de la lumière diffuse de LIGHT0 est augmentée (respectivement diminuée). La variable concernée est light_diffuse.
        • Si l'utilisateur presse la touche "a" (respectivement "A"), l'intensité de la lumière ambiante de LIGHT0 est augmentée (respectivement diminuée). La variable concernée est light_ambiant.
        • Si l'utilisateur presse la touche "r" (respectivement "R"), la taille du reflet de la matière est augmenté (respectivement diminué). La variable concernée est mat_shininess.
        • Si l'utilisateur presse la touche "g" (respectivement "G"), l'intensité de la lumière ambiante générale est augmentée (respectivement diminuée). La variable concernée est general_light_ambiant.
        • Si l'utilisateur presse les touches x,y ou z (respectivement X,Z ou Z), la position de la lumière est modifiée. La variable concernée est light_position.
      3. Exécutez votre programme ainsi modifié en variant les différents paramètres d'éclairage afin de comparer les différents types de lumière (spéculaire, diffuse, ambiante ...). Pourquoi la sphère est elle grise ?
      4. Dans le programme précédent, il s'agissait d'une lumière blanche. Compte tenu des propriétés de matière, la sphère était grise. Modifiez le programme de la question 3 de sorte que la lumière émise par la source soit de couleur rouge (cf. programme exo12q2 ). Testez à nouveau le comportement de l'éclairage en modifiant les différents paramètres d'intensité, de position ou de réflexivité de la lumière.




      Exercice 13 : scène avec plusieurs sources lumineuses

      Dans cet exercice, on utilise deux sources lumineuses (LIGHT0 et LIGHT1).
      1. Ecrire un programme qui restitue 3 sphères jaunes dont deux qui effectuent une rotation autours de la troisième (voir l'exécutable exo13q1 ). Attention : pour pouvoir utiliser l'éclairage, il est nécessaire de décrire les objets avec leurs normales de surface. Pour ce faire, il est conseillé de partir du programme exo12.c qui contient ces vecteurs pour une sphère (cf. primitives glNormal3f dans la fonction draw_triangle).
      2. Modifiez votre programme de sorte que (cf. exécutable exo13q2 ) :
        • Une des sphères en rotation est éclairée par une lumière rouge (LIGHT0).
        • L'autre sphère en rotation est éclairée par une lumière verte (LIGHT1).
        • La sphère immobile n'est pas éclairée.
        • Les deux sources de lumière sont positionnées en (-7.0, 2.0, 5.0, 1.0).
        • Les propriétés de matière pour toutes les sphères sont les suivantes : réfléxivité ambiante : (0.7, 0.7, 0.7, 1.0) ; réfléxivité diffuse : (0.1, 0.1, 0.1, 1.0) ; réfléxivité spéculaire : (1, 1, 1, 1) ; pas de lumière émise ; taille du reflet : 5 pour une des sphères éclairées, 70 pour l'autre sphère éclairée.
        • La lumière ambiante générale est de (0.2, 0.2, 0.2, 1.0).






      IV. Projet à rendre



      Projet 2016/2017



      Le but du projet est de contruire une application qui fait la synthèse des différents concepts présentés dans la partis "OpenGL". Votre programme devra au moins illustrer les aspects suivants :
      1. Utilisation des primitives géométriques,
      2. Transformation de modèle, de projection et de visualisation,



      Figure 15. Jeu du puissance 4 en 3D


      Le sujet du projet consiste a réaliser un jeu de puissance 4 (cf. figure ci-dessus). Ce jeu de puissance 4 a comme particularité d'être en 3D. Les principale règles du jeu sont les suivantes :
      • Il y a 32 boules claires et 32 boules foncées.
      • Le plateau contient 16 tiges. Chaque tige peut contenir 4 boules.
      • Pour gagner, un joueur doit aligner 4 boules. Les boules peuvent être alignées horizontalement, verticalement ou en diagonale et sur n'importe quel étage des tiges.
      • La partie est nulle si toutes les boules sont posées et si aucun joueur n'a réussi à aligner 4 boules.
      Que ce soit sur l'animation, sur l'esthétique du jeu, ou sur les règles du jeu, vous pouvez laisser libre cours à votre imagination.

      Le projet devra être remis avant le 31 mars par mail à Frank Singhoff. Une démonstration sera organisée le 31 mars. Durant cette soutenance, vous décrirez votre travail (fonctionnalités, conception détaillée, état d'avancement, techniques et effets graphiques/sonores utilisés, ...). Vous devez obligatoirement utiliser le matériel/logiciel utilisé pendant les cours.

      Vous pouvez travailler en groupe de 2 à 3, mais à condition de bien décrire le travail de chacun. Vous ne devrez pas utiliser de code autre que celui offert par les bibliothèques gl, glu et glut (pas de code téléchargé depuis le web !).

      Projet 2015/2016



      Le but du projet est de construire une application qui fait la synthèse des différents concepts présentés dans le cours d'OpenGL. Votre programme devra au moins illustrer les aspects suivants :
      1. Utilisation des primitives géométriques,
      2. Opérations sur les sommets (transformations), opérations sur les pixels (textures et éclairage),



      Le Morpion 3D



      Vous pouvez travailler en binome ou seul (mais pas plus de deux étudiants par groupe). La note constituera une partie de la note de CC de l'UE Multimédia et animation (15 % de la note d'UE).

      Chaque groupe doit réaliser un jeu de type Morpion, mais en 3D. Pour plus de précisions, consultez l'article de wikipedia consacré à ce : type de jeu. Extrait :

      Le morpion est un jeu de réflexion se pratiquant à deux joueurs au tour par tour et dont le but est de créer le premier un alignement sur une grille. Le jeu se joue généralement avec papier et crayon. Il existe de nombreuses variations de ce jeu, y compris en 3D, et cette multiplicité se décline sur tous les types d'ordinateurs. L'image JPEG ci-dessus en est un exemple.

      Travail à réaliser

      Vous pouvez vous inspirer de jeux existants. Le sujet est assez libre pour ce qui est des fonctionnalités ou de l'esthétisme. Vous pouvez laisser libre cours à votre imagination, à condition que vous respectiez les contraintes ci-dessous.

      Vous devez obligatoirement utiliser le logiciel utilisé pendant les cours : vous ne devrez pas utiliser de code autre que celui offert par les bibliothèques gl, glu et glut et pas de code téléchargé depuis le web !

      Le projet devra être remis pour le 1er Avril 2016 au plus tard, par mail à Frank Singhoff. Une démonstration sera organisée le 1er avril 2016 matin (s'inscrire sur la porte de F. Singhoff). Durant cette soutenance, vous décrirez votre travail. Vous serez évalués sur les critères suivants : les fonctionnalités, la conception détaillée, l'état d'avancement, les techniques et effets graphiques utilisés, la qualité du code (propreté, fiabilité), la documentation. La qualité de la documentation (manuel d'utilisation, conception logicielle, description de la conduite des tests) sera prépondérante pour la notation.





      Projet 2014/2015



      Le but du projet est de construire une application qui fait la synthèse des différents concepts présentés dans le cours d'OpenGL. Votre programme devra au moins illustrer les aspects suivants :
      1. Utilisation des primitives géométriques,
      2. Opérations sur les sommets (transformations), opérations sur les pixels (textures et éclairage),



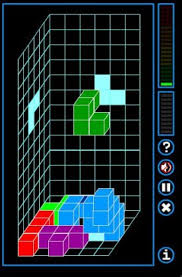
      Exemples de Tetris 3D



      Vous pouvez travailler en binome ou seul (mais pas plus de deux étudiants par groupe). La note constituera une partie de la note de CC de l'UE Multimédia et animation (15 % de la note d'UE).

      Chaque groupe doit réaliser un jeu de type Tetris. Pour plus de précisions, consultez l'article de wikipedia consacré à ce type de jeu : http://fr.wikipedia.org/wiki/Tetris. Extrait :

      Tetris est un jeu vidéo de puzzle conçu en 1984[1],[2],[3] par Alexei Pajitnov. Bâti sur des règles simples et exigeant intelligence et adresse, il est l'un des jeux vidéo les plus populaires au monde. Ses versions sont innombrables, y compris en 3D, et cette multiplicité se décline sur tous les types d'ordinateurs.

      Travail à réaliser

      Vous pouvez vous inspirer de jeux existants. Le sujet est assez libre pour ce qui est des fonctionnalités ou de l'esthétisme. Vous pouvez laisser libre cours à votre imagination, à condition que vous respectiez les contraintes ci-dessous.

      Vous devez obligatoirement utiliser le logiciel utilisé pendant les cours : vous ne devrez pas utiliser de code autre que celui offert par les bibliothèques gl, glu et glut et pas de code téléchargé depuis le web !

      Le projet devra être remis pour la semaine du 16 mars 2015 au plus tard, par mail à Frank Singhoff. Une démonstration sera organisée après le 16 mars 2015. Durant cette soutenance, vous décrirez votre travail. Vous serez évalués sur les critères suivants : les fonctionnalités, la conception détaillée, l'état d'avancement, les techniques et effets graphiques utilisés, la qualité du code (propreté, fiabilité), la documentation. La qualité de la documentation (manuel d'utilisation, conception logicielle, description de la conduite des tests) sera prépondérante pour la notation.





      Projet 2013/2014



      Le but du projet est de contruire une application qui fait la synthèse des différents concepts présentés dans la partie OpenGL de l'UE Multimédias et animation. Votre programme devra au moins illustrer les aspects suivants :
      1. Utilisation des primitives géométriques,
      2. Opérations sur les sommets (transformations), opérations sur les pixels (textures et éclairage),



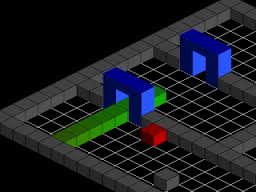
      Exemples de Snake 3D


      Le sujet du projet consiste a réaliser un jeu vidéo en 3D inspiré de Snake. L'historique de ce jeu ainsi que son fonctionnement général peuvent être consultés à cette adresse.

      Bien sûr, il existe de nombreuses variations possibles pour ce jeu, que ce soit sur l'animation, sur la façon dont la 3D est utilisée, les règles du jeu, ... La figure ci-dessus présente différents exemples de Snake qui peuvent vous inspirer pour la réalisation du jeu vidéo. Vous pouvez laisser libre cours à votre imagination, à condition que vous respectiez les contraintes suivantes :

      1. Le projet devra être remis pour le 31 mars 2013 au plus tard, par mail à Frank Singhoff. Une démonstration sera organisée la semaine du 31 mars. Durant cette soutenance, vous décrirez votre travail. Vous serez évalués sur les critères suivants : les fonctionnalités, la conception détaillée, l'état d'avancement, les techniques et effets graphiques utilisés, la qualité du code (propreté, fiabilité), la documentation. La qualité de la documentation (manuel d'utilisation, conception logicielle, description de la conduite des tests) sera prépondérante pour la notation.
      2. Vous devez obligatoirement utiliser le matériel/logiciel utilisé pendant les cours : vous ne devrez pas utiliser de code autre que celui offert par les bibliothèques gl, glu et glut pour ce qui est de la restitution 3D (pas de code téléchargé depuis le web !) sur Linux uniquement. Les démonstrations doivent pouvoir être effectuées sur les machines des salles de TP. Les projets utilisant d'autres plate-formes de développement ne seront pas évalués.
      3. Vous pouvez travailler en binome ou seul (mais pas plus de deux étudiants par groupe). La note constituera une partie de la note de CC de l'UE Multimédia et animation (15 % de la note d'UE).




      Projet 2012/2013



      Le but du projet est de contruire une application qui fait la synthèse des différents concepts présentés dans la partie OpenGL de l'UE Multimédias et animation. Votre programme devra au moins illustrer les aspects suivants :
      1. Utilisation des primitives géométriques,
      2. Opérations sur les sommets (transformations), opérations sur les pixels (textures et éclairage),



      Figure 12. Différents exemples de Pac-Man


      Le sujet du projet consiste a réaliser un jeu vidéo en 3D inspiré de Pac-Man. L'historique de ce jeu ainsi que son fonctionnement général peuvent être consultés à cette adresse.

      Bien sûr, il existe de nombreuses variations possibles pour ce jeu, que ce soit sur l'animation, sur la façon dont la 3D est utilisée, les règles du jeu, ... La figure 12 présente différents exemples de Pac-Man qui peuvent vous inspirer pour la réalisation du jeu vidéo. Vous pouvez laisser libre cours à votre imagination, à condition que vous respectiez les contraintes suivantes :

      1. Le projet devra être remis pour le 15 février 2013 au plus tard, par mail à Frank Singhoff. Une démonstration sera organisée en février. Durant cette soutenance, vous décrirez votre travail. Vous serez évalués sur les critères suivants : les fonctionnalités, la conception détaillée, l'état d'avancement, les techniques et effets graphiques utilisés, la qualité du code (propreté, fiabilité), la documentation. La qualité de la documentation (manuel d'utilisation, conception logicielle, description de la conduite des tests) sera prépondérante pour la notation.
      2. Vous devez obligatoirement utiliser le matériel/logiciel utilisé pendant les cours : vous ne devrez pas utiliser de code autre que celui offert par les bibliothèques gl, glu et glut (pas de code téléchargé depuis le web !) sur Linux uniquement. Les démonstrations doivent pouvoir être effectuées sur les machines des salles de TP. Les projets utilisant d'autres plate-formes de développement ne seront pas évalués.
      3. Vous pouvez travailler en binome ou seul (mais pas plus de deux étudiants par groupe). La note constituera une partie de la note de CC de l'UE Multimédia et animation (15 % de la note d'UE).




      Projet 2011/2012



      Le but du projet est de contruire une application qui fait la synthèse des différents concepts présentés dans la partie OpenGL de l'UE Multimédias et animation. Votre programme devra au moins illustrer les aspects suivants :
      1. Utilisation des primitives géométriques,
      2. Opérations sur les sommets (transformations), opérations sur les pixels (textures et éclairage),



      Figure 12. Différents exemples de Rubik's cube


      Le sujet du projet consiste a réaliser un casse-tête tel que le Rubik's cube. On vous demande d'implanter ce jeu en 3D. L'historique de ce jeu ainsi que son fonctionnement général peuvent être consultés à cette adresse.

      Bien sûr, il existe de nombreuses variations possibles pour ce casse-tête, que ce soit sur l'animation, sur la forme et la taille du casse-tête, les couleurs, ... La figure 12 présente différents exemples de Rubik"s cube qui peuvent vous inspirer pour la réalisation du jeu vidéo. Vous pouvez laisser libre cours à votre imagination, à condition que vous respectiez les contraintes suivantes :

      1. Le projet devra être remis pour le 9 février 2012 au plus tard, par mail à Frank Singhoff. Une démonstration sera organisée le 9 février. Durant cette soutenance, vous décrirez votre travail. Vous serez évalués sur les critères suivants : les fonctionnalités, la conception détaillée, l'état d'avancement, les techniques et effets graphiques utilisés, la qualité du code (propreté, fiabilité), la documentation. La qualité de la documentation (manuel d'utilisation, conception logicielle, description de la conduite des tests) sera prépondérante pour la notation.
      2. Vous devez obligatoirement utiliser le matériel/logiciel utilisé pendant les cours : vous ne devrez pas utiliser de code autre que celui offert par les bibliothèques gl, glu, glut et SDL (pas de code téléchargé depuis le web !) sur Linux uniquement. Les effets graphiques seront codés avec les bibliothèques gl, glu, glut. Les démonstrations seront effectuées sur les machines de salles de TP. Les projets utilisant d'autres plate-formes de développement ne seront pas évalués.
      3. Vous pouvez travailler en binome ou seul (mais pas a plus de deux étudiants). La note constituera une partie de la note de CC de l'UE Multimédia et animation (15 % de la note d'UE).




      Projet 2010/2011



      Le but du projet est de contruire une application qui fait la synthèse des différents concepts présentés dans la partis "OpenGL". Votre programme devra au moins illustrer les aspects suivants :
      1. Utilisation des primitives géométriques,
      2. Transformation de modèle, de projection et de visualisation,



      Figure 14. Exemple d'un jeu de bataille navale sur plateau


      Le sujet du projet consiste a réaliser un jeu de bataille navale. On vous demande d'implanter ce jeu en 3D. La bataille navale est un jeu de société dans lequel deux joueurs doivent placer des bateaux sur une grille tenue secrète et tenter de se les 'torpiller' mutuellement. Ce jeu a été rendu populaire en 1931 dans les publications américaines de divertissement de la Milton Bradley Company (devenue MB, cf Wikipedia).

      Chaque joueur possède les mêmes bateaux, dont le nombre et le type dépendent des règles du jeu choisies. Une disposition classique peu ainsi comporter :
      • 1 porte-avions (5 cases)
      • 1 croiseur (4 cases)
      • 1 contre-torpilleur (3 cases)
      • 1 sous-marin (3 cases)
      • 1 torpilleur (2 cases)
      Chaque joueur dispose devant lui de 2 grilles de jeu (cf. Figure 14). Une grille de jeu est numérotée de 1 à 10 horizontalement et de A à J verticalement. Conventionnellement, les joueurs placent des pions blancs sur la première grille (cf. grille du haut sur la Figure 14) lorsque les coordonnées n'ont pas touché de bateau adverse, et rouge lorsqu'une touche a été faite. La seconde grille (grille du bas sur la Figure 14) mémorise la place des bateaux du joueur et indique, par des pions rouges les bateaux qui ont été coulés par l'adversaire. Bien sûr, il existe de nombreuses variations possibles sur ces règles du jeu : que ce soit sur l'animation, sur l'esthétique du jeu, ou sur les règles du jeu, vous pouvez laisser libre cours à votre imagination, à condition que vous respectiez les contraintes suivantes :

      Le projet devra être remis avant le 17 janvier par mail à Frank Singhoff. Une démonstration sera organisée en janvier. Durant cette soutenance, vous décrirez votre travail (fonctionnalités, conception détaillée, état d'avancement, techniques et effets graphiques utilisés, ...). Vous devez obligatoirement utiliser le matériel/logiciel utilisé pendant les cours : vous ne devrez pas utiliser de code autre que celui offert par les bibliothèques gl, glu et glut (pas de code téléchargé depuis le web !) sur Linux uniquement. Les effets graphiques seront codés avec les bibliothèques gl, glu, glut.

      Vous pouvez travailler en binome (mais pas a plus de deux étudiants). La note constituera la note de CC pour OpenGl de l'UE Multimédia et animation (soit 15 % de la note d'UE).



      Projet 2007/2008



      Le but du projet est de contruire une application qui fait la synthèse des différents concepts présentés dans les parties "OpenGL" et "traitement du son". Votre programme devra au moins illustrer les aspects suivants :
      1. Utilisation des primitives géométriques,
      2. Opérations sur les sommets (transformations), opérations sur les pixels (textures et éclairage),
      3. Sonnorisation des événements.



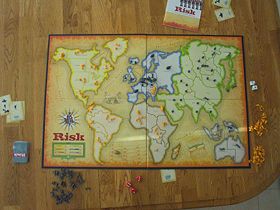
      Figure 13. Exemple d'un jeu stratégie sur plateau


      Le sujet du projet consiste a réaliser un jeu de stratégie tel que Risk. On vous demande d'implanter ce jeu en 3D. Risk est un jeu de société dans lequel plusieurs joueurs (en général, au moins 3) doivent atteindre un objectif secret. L'historique de ce jeu ainsi que son fonctionnement général peuvent être consultés à cette adresse. Les règles détaillées du jeu Risk peuvent être lues à cette adresse.

      Le principe général de ce jeu de société est le suivant:
      • Le plateau présente une carte politique stylisée du monde divisée en 42 territoires groupés en 6 continents.
      • Pour commencer, un des joueurs distribue chacun des pays. Chaque joueur y place une ou plusieurs armées.
      • Puis, chaque joueur se voit assigner une mission. On ne connait pas la mission de son adversaire, mais on doit essayer de la deviner en fonction de la stratégie de jeu de celui-ci. Ainsi, en fonction de sa mission, ou non s'il veut bluffer, les joueurs placent leurs fantassins sur leurs pays, sans limite d'effectif, avec un minimum de 1 fantassin par pays.
      • Le jeu consiste à allouer des armées dans les territoires contrôlés puis attaquer les zones voisines pour les conquerir. La résolution des combats est décidée en jetant un, deux ou trois dés par joueur participant au combat.
      • Le jeu est terminé quand l'un des joueurs a atteint son objectif.


      Bien sûr, il existe de nombreuses variations possibles sur ces règles du jeu : que ce soit sur l'animation, sur l'esthétique du jeu, ou sur les règles du jeu, vous pouvez laisser libre cours à votre imagination, à condition que vous respectiez les contraintes suivantes :

      1. Le projet devra être remis pour le 17 décembre au plus tard, par mail à Frank Singhoff. Une démonstration sera organisée le jeudi 17 décembre. Durant cette soutenance, vous décrirez votre travail. Vous serez évalués sur les critères suivants : les fonctionnalités, la conception détaillée, l'état d'avancement, les techniques et effets graphiques/sonores utilisés, la qualité du code (propreté, fiabilité), la documentation.
      2. Vous devez obligatoirement utiliser le matériel/logiciel utilisé pendant les cours : vous ne devrez pas utiliser de code autre que celui offert par les bibliothèques gl, glu, glut et SDL (pas de code téléchargé depuis le web !) sur Linux uniquement. Les effets graphiques seront codés avec les bibliothèques gl, glu, glut. Les effets sonores seront codés avec la bibliothèque SDL. Les projets utilisant d'autres plate-formes de développement ne seront pas évalués.
      3. Vous pouvez travailler en binome ou seul (mais pas a plus de deux étudiants). La note constituera la note de CC de l'UE Multimédia et animation (50 % de la note d'UE).










      IV. Exercices supplémentaires





      Exercice 14 : transformations : rotations avec glRotate

      A partir de l'approximation de sphère de l'exercice 9, on vous demande de construire un programme simulant le système solaire.


      PLANETE Mercure Vénus Terre Mars Jupiter Saturne Uranus Neptune Pluton
      distance moyenne au Soleil
      (millions de km)      		581081502287781427287045005950
      Durée d'une révolution
      (années)      		0,240,6111,8811,8629,4584164247,7
      Durée de la rotation
      		59 j243 j23h 56min24h 37 min9h 50min10h 39min17h 14min16h 3min153h 17min
      Inclinaison axe rotation (degrés)
      		0177,323,423,983,126,797,929,694
      Rayon
      (km)      		2420620063783400714006040023800223002920

      Figure 6. Informations pour chaque planète


      Figure 7. Sens de rotation des planètes

      1. Sachant que le rayon du soleil est de 69000 kms et compte tenu des différentes tailles des planètes, écrire un programme où le soleil et chaque planète sont modélisés par une sphère (par transformation de modèle). Respectez au mieux, pour chaque sphère, les tailles et distances entre les différents objets célestes. Lorsque les grandeurs d'ordre sont trop différentes (exemple : tailles des sphères vis-à-vis des distances entre elles), optez pour une solution qui reste cohérente.
      2. Chaque planète effectue une révolution. On suppose strictement circulaire chaque révolution autour du soleil. Modifiez votre programme afin de modéliser ces déplacements (par transformation de modèle).
      3. Chaque planète effectue une rotation sur elle même dans un axe donné. Modifiez votre programme afin de modéliser ces rotations (par transformation de modèle).




      Exercice 11 : textures procédurales

      Dans cet exercice, on construit une petite texture procédurale. Il s'agit d'une texture dont les texels sont construits par un algorithme (généralement, une fonction mathématique) plutôt qu'une texture obtenue par numérisation.
      Soit le programme exo11q1.c
        Ce programme restitue un carré texturé. Compilez, testez et étudiez ce programme.
      • Dans quelle variable est construite/stockée la texture ?
      • Quelle est la taille de la texture ?
      • Modifiez et testez les valeurs de pixel[i][j][0], pixel[i][j][1] et pixel[i][j][2]. Comment est mémorisée la couleur de chaque pixel dans la texture ?


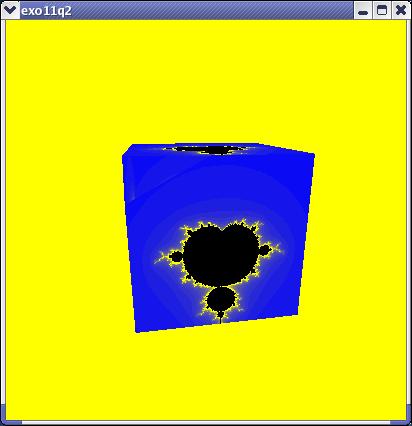
      Figure 11. Texture Mandelbrot




      Afin d'illustrer les textures procédurales, on souhaite maintenant construire une texture basée sur l'ensemble de Mandelbrot. On considère le programme exécutable exo11q2 . Ce programme restitue un cube dont certaines faces sont texturées avec une texture procédurale qui représente l'ensemble de Mandelbrot. L'ensemble de Mandelbrot est un ensemble de complexes déterminé par la suite Zn+1=Zn*Zn + c avec Z0=0. Cet ensemble de complexes est représenté par une fractale (courbe fermée de longueur infinie dont aucun point n'admet de tangente). C'est cette fractale qui constitue la texture à construire.

      Soit le programme exo11q2.c . Complétez de la façon suivante :
      1. Implantez la fonction mandel. Cette fonction prend en paramètre un complexe C défini par le couple (cx,cy). Cette fonction implante le calcul des nb_iteration premiers éléments de la suite Zn. On rappelle que si z et z' sont des complexes définis par les couples (x,y) et (x',y'), alors :
        z+z'=(x,y)+(x',y')=(x+x', y+y')
        z.z'=(x,y).(x',y')=(xx'-yy', xy'+x'y)
        Pour chaque itération, la fonction mandel doit comparer la valeur du complexe calculé à un réel qui constitue un seuil. Soit z un complexe défini par le couple (x,y). Le réel correspondant à z est égal au réel x * x + y * y. C'est ce réel qui devra être comparé au seuil. Dans le cas où le complexe calculé (c-a-d sa réprésentation réelle) est supérieur au seuil, alors la fonction retourne immédiatement le numéro d'itération. Si toute les itérations sont calculées sans atteindre le seuil, alors la fonction renvoit -1.
      2. Appliquez la fonction mandel à chaque pixel. La texture à construire est une texture de 256x256 pixels. Chaque pixel représente un nombre complexe (x,y) tel que x et y appartiennent à [0,3]. Par exemple, le pixel en haut à gauche de la texture représente le nombre complexe (0,0) et le pixel en bas à droite, le nombre complexe (3,3) (avec cette solution, l'ensemble de MandelBrot ne sera pas centré comme dans l'exécutable donné en exemple). La variable pixel stocke en fait pour chaque nombre complexe, la valeur -1 s'il appartient à l'ensemble de MandelBrott ou une valeur décrivant sa distance vis-à-vis de l'ensemble.
      3. Déterminez la couleur de chaque pixel . Pour chaque pixel, si la valeur de la variable pixel est négative, on associe la couleur noire dans la texture. Si la valeur est positive, on positionne la couleur de cette façon :
        • les composantes R et G doivent être égale au minimum entre 255 est pixel[i][j]*10,
        • la composante B doit être égale à 255 - R.
      4. Derniere opération : Visionnez le cube ainsi restitué !!! Testez le programme avec des valeurs différentes du nombre d'itérations ou du seuil (valeurs inférieures conseillées).