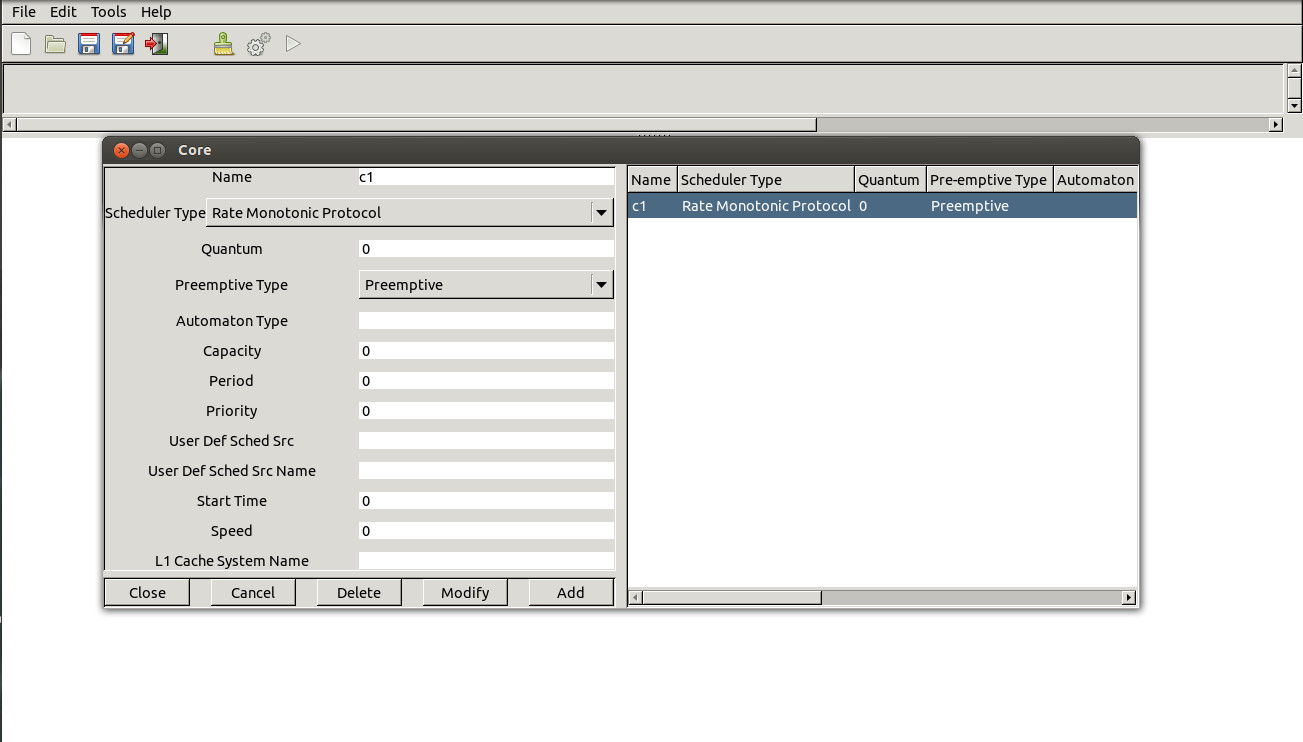
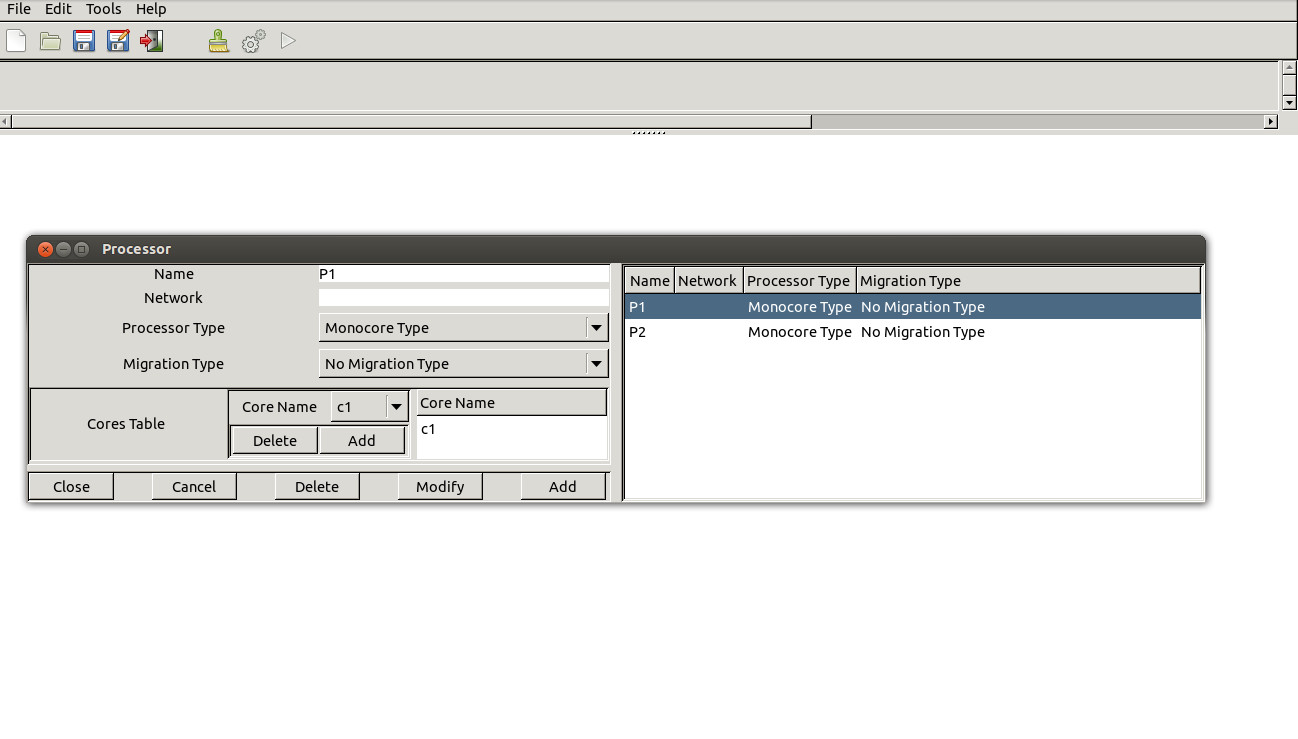
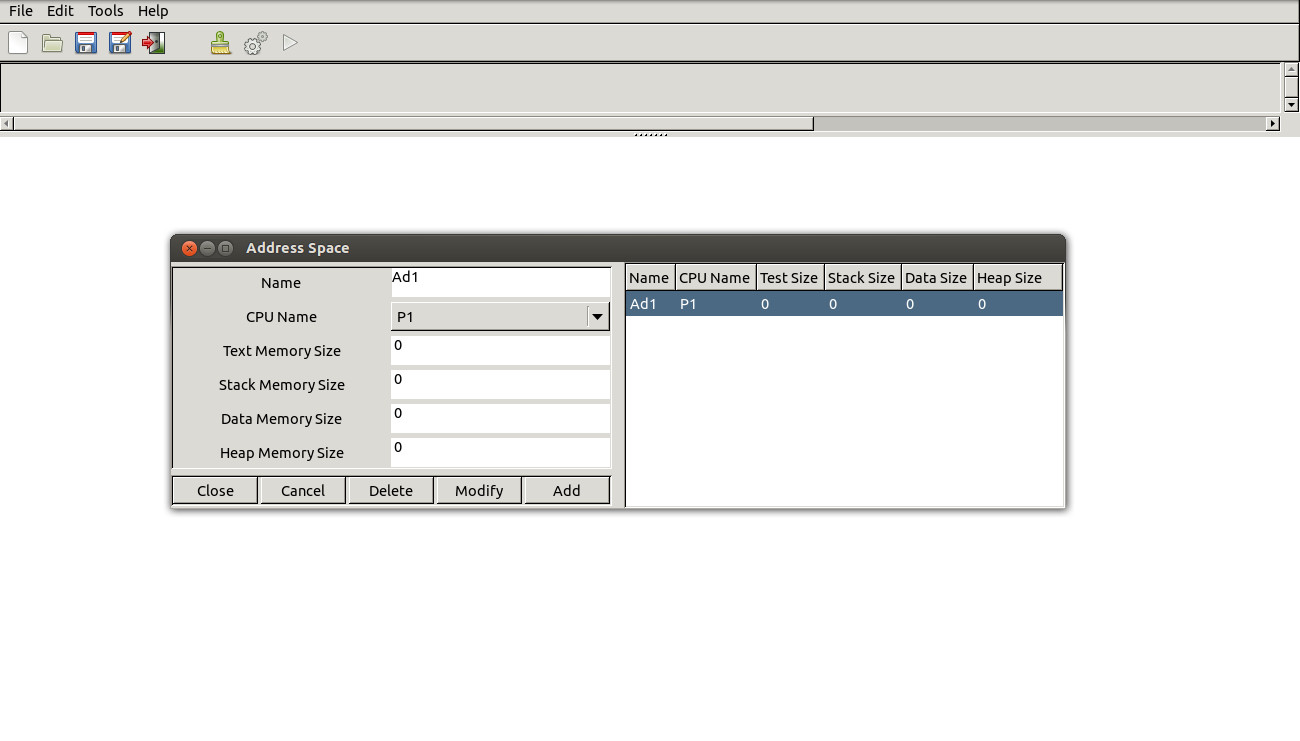
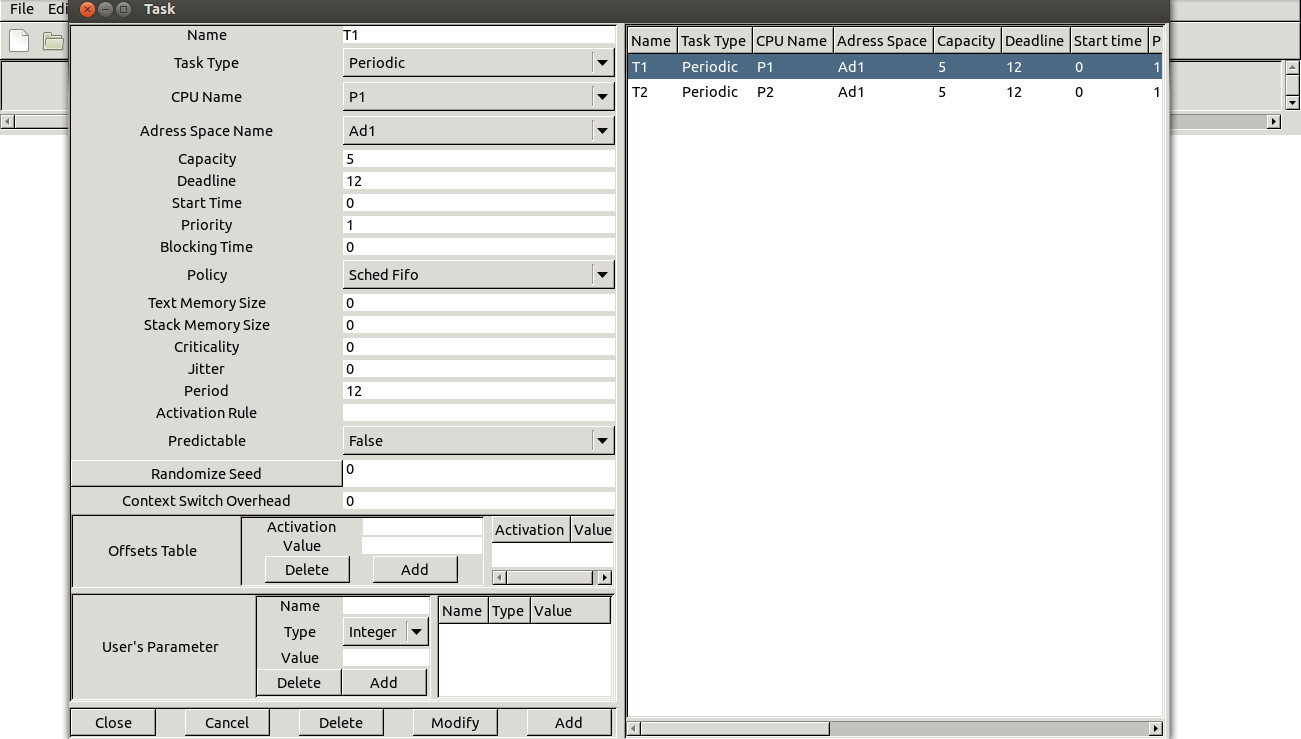
Cheddar provides supports for modeling the CFG of a task. An external tool is used to parse the object file of a task and then to compute and generate the CFG in a Cheddar-compatible format. Examples of the CFGs computed for tasks in the Malardalen benchmark are available on the Cheddar svn repository at this link.
The users can import an existing system model with several tasks in Cheddar or choose to create a new model.
After that, the CFGs of these tasks can imported by Cheddar :
Menu --> Tools --> Cache --> Import Control Flow Graph- If the users import a Cheddar-ADL system model, the CFGs must be located in the same folder as the xml file.
- If the users create a new system model, the CFGs must be located in the same folder with the Chedder executable file.
- The attribute "cfg_name" is used to associate a CFG to a task. The xml file contains the CFG must has the same name as Cheddar automatically search for the CFGs to be imported.
The current GUI of Cheddar does not provide an interactive way to work (add/modify/delete) with CFGs. The features are to be implemented in the next version.
The sets of UCBs and ECBs of a program are computed by Cheddar from its CFG.
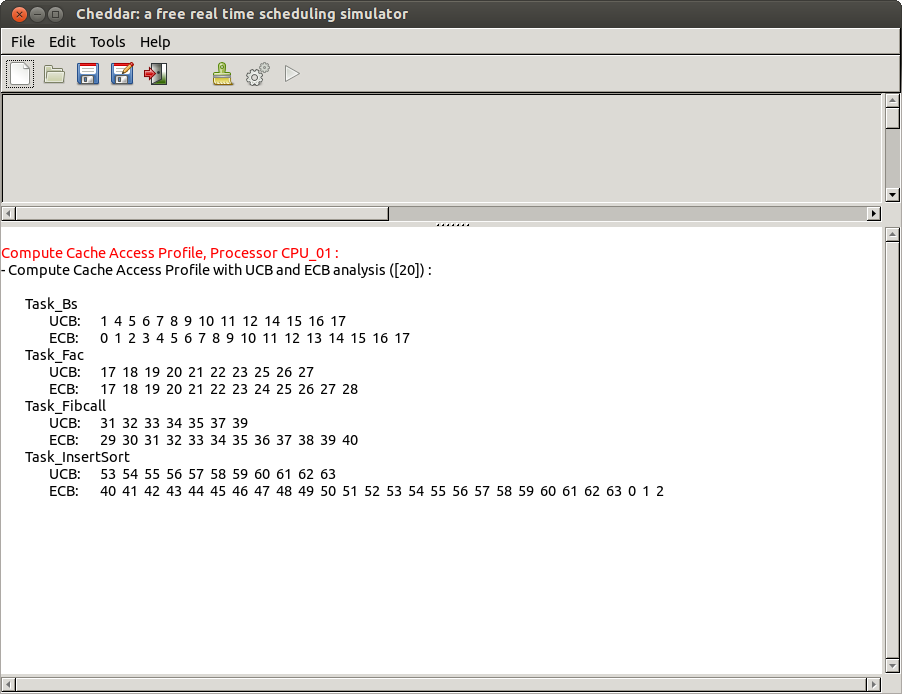
The sets of UCBs and ECBs can also be computed by external tools and put directly in Cheddar without passing by this step. In order to do this, the users need to modify the xml file of a Cheddar-ADL system model with the information about the UCBs and ECBs of tasks.
After this step, the following analyses are available in CheddarIn order to perform CRPD-Aware WCRT analysis in Cheddar, the following steps are required:
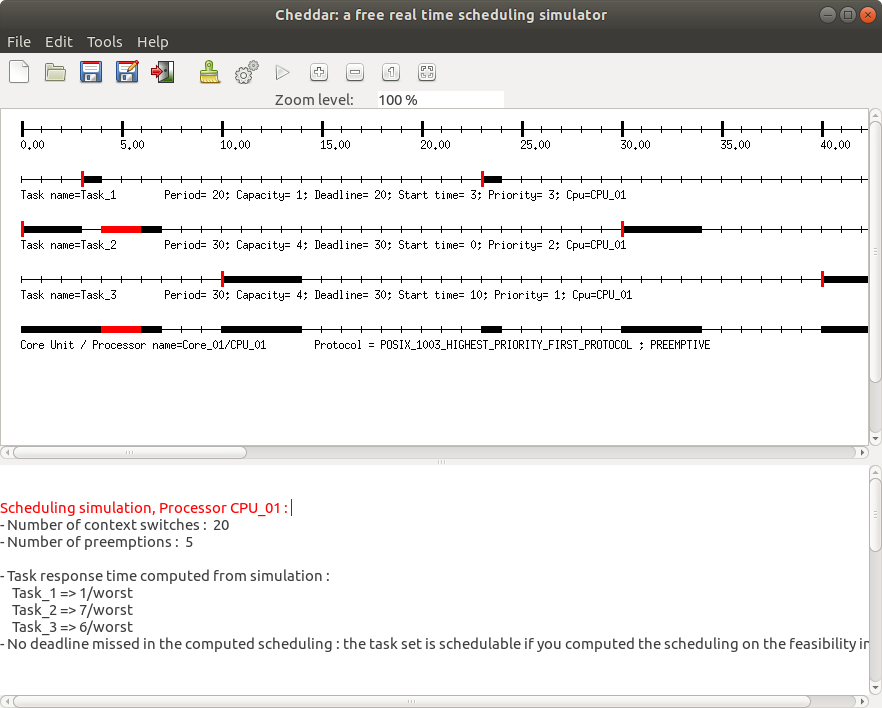
In order to perform CRPD-aware scheduling simulation in Cheddar, the following steps are required.
- The set of UCBs and ECBs of all tasks must be computed (Step 3).
- Check the CRPD check box in
Tools --> Scheduling --> Scheduling Options - Run the simulation. The CRPD added to the capacities of tasks are represented by the red blocks (as shown in the image below)
Our implementation of the CRPD-aware priority assignment is based on Audsley's Optimal Priority Assignment (OPA) algorithm. We extended this algorithm in order to take into account the CRPD. In order to perform CRPD-aware prority assignment in Cheddar, the following steps are required.
- The set of UCBs and ECBs of all tasks must be computed (Step 3).
Tools --> Scheduling --> Scheduling Options --> Tasks Priority Assignment-
The following CRPD priority assignment algorithms, which are detailed in the referenced article, are available in Cheddar:
- CRPD OPA-PT
- CRPD OPA-PT Simplified
- CRPD OPA-PT Tree

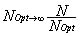 .
.
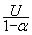 , a = max Ui, i = 1,�,K and U is
utilization of all tasks. Tasks are sorted in increasing Si. Si =
log2(Ti). The main idea of RMST is to minimize the value of
b for each processor. � = max Si � min Si, 1= i =K.
, a = max Ui, i = 1,�,K and U is
utilization of all tasks. Tasks are sorted in increasing Si. Si =
log2(Ti). The main idea of RMST is to minimize the value of
b for each processor. � = max Si � min Si, 1= i =K.